Created with help of Mosh

Big O notation

Big O uses to describe the performance of an algorithm
lim->imfinity

  • Constant O(1)
    O(1+1+…+n) = O(1)
  • Linear O(n)
    O(n+n+…+n) = O(n)
  • Quadratic O(n^2)
    O(n + n^2) = O(n^2)
  • Logarithmic O(log n)
  • Exponential O(2^n) image of big O

Arrays

O

  • Lookup
    • by index O(1)
    • by value O(n)
  • Insert O(n)
  • Delete O(n)

Implementations

  • ArrayList
  • Vector

Linked List

O

  • Lookup
    • by index O(n)
    • by value O(n)
  • Insert
    • Head O(1)
    • Tail O(1)
    • Middle O(n)
  • Delete
    • Head O(1)
    • Tail O(n)
    • Middle O(n)

Implementations

  • LinkedList
  • Implement
  • Find Middle (without size) in one path
  • Find kth element from end (without size) in one path
  • Check if has loop

Stack

Last in First out (LIFO)

O

All operation runs in O(1)

Implementations

  • Stack
  • Implement
  • Reversing strings
  • Balanced expressions (if has closed brackets -> { [<>] ()} –> true)
  • Min Stack

Queues

First in First out (FIFO)

O

All operation runs in O(1)

Implementations

  • ArrayDeque, LinkedList
  • Implement
  • Reversing a queue (only with add, remove, isEmpty)
  • Implement a queue with array (hint: circular array)
  • Implement a queue with stack

HashTable

Key and Value pair

Map can store null in keys and values in Java

Handle Collisions

  • chaining (put items in a list)
  • oppen addrasing
    • linear probing (makes a claster, so with time handling collisions will be slower)
      (hash(key) + i) % table_size
    • quadratic probing (it’s slolves cluster problem, but has a chance to fall in an infinitive loop)
      (hash(key) + 1^2) % table_size
    • double hashing
    hash2(key) = prime - (key % prime)  // something that works (prime -> prime number smaller than table size)
(hash1(key) + i * hash2(key)) %  table_size

O

All operation runs in O(1)
Very very very hardly ever O(n) because Implemented using Arrays
O(n) almost never happend so speed is O(1)

Implementations

  • HashMap, HashSet
  • Implement
  • Find the first non-repeated character in a string
  • Find the first repeated character in a string
  • Find most frequent element in array
  • Get number of pairs with difference K
  • Get indices of the two numbers with sum K

Binary Searched Tree

l e a f R o o t l e a f

Traversing

1 4 6 7 8 9 1 0

  • Breadth First level order

    7, 4, 9, 1, 6, 8, 10

  • Depth First

    • Pre-orderRoot, left, right

    7, 4, 1, 6, 9, 8, 10

    • In-order left, Root, right

    1, 4, 6, 7, 8, 9, 10

    • Post-order left, right, Root

    1, 6, 4, 8, 10, 9, 7

  • Depth

4 ( 1 7 ) ( 0 ) 9 ( 1 )
  • Height
4 ( 1 7 ) ( 3 ) 9 ( 1 1 0 ) ( 0 )

O

  • Lookup O(log n)
  • Insert O(log n)
  • Delete O(log n)

tree can have O(n)
if not structured properly

h (height) = O(log n) » O(h) == O(log n)

Implementations

  • Implement
  • Traversing (pre-, in-, post- order, and level order)
  • Get Min value (recursion and loop)
  • Check if tree is equal to another tree
  • Check if is Binary Search tree (every left child is less, and right shild is greater than ancestor)
  • Print Nodes at K Distance
  • Calculate size
  • Count the number of leaves in a binary tree
  • Are elements siblings (3 < 5 > 7 -> 3 and 7 are siblings)
  • Get Ancestors of a value (in List)

AVL Trees

Worst case scenario when tree becomes right/left skewed

1 > 2 > 10 > 100 -> right skewed tree

Self-balancing trees

  • AVL Trees
  • Red-black Trees
  • etc.

Rotations

  • left
0 1 0 2 2 0 1 3 0 1 2 3
  • right
1 2 3 1 2 3
  • left-right
5 9 7 5 7 9 5 7 9
  • right-left
5 7 1 0 5 7 1 0 5 7 9

Visualize online

O

  • Lookup O(log n)
  • Insert O(log n)
  • Delete O(log n)

Implementations

  • Draw rotation
  • Check if balanced (difference of every node’s height of left sub-tree and right sub-tree less than 2)
  • Is perfect (every leaf is full and leaves depth is the same)
5 5 3 0 2 5 4 0 3 5 5 0 5 5 i s p e r f e c t

Heaps

Special tipe of tree that is

  • complete

All levels except the last one should be full of nodes, and
nodes are inserted from left to right

  • all child less than ancestor

called heap property

( c o m p l e t e ) ( n o t c o m p l e t e )

How a MaxHeap will insert [40, 30, 20, 50]

4 0 3 0 4 0 3 0 4 0 2 0

Bubling up

3 5 3 0 0 0 4 3 5 0 0 0 5 4 4 0 0 0 2 2 2 0 0 0

Bubling down

3 0 4 0 5 0 2 0 4 0 3 0 2 0 3 0 4 0 2 0

in this example we’ll remove 50

O

  • Lookup
    • max (min) O(1)
  • Insert O(log n)
  • Delete O(log n)

Implementations

  • Implement
  • Heapify regular array
  • Get Kth larges item

{5, 3, 8} > k = 1 -> 8

  • Check if array represents MaxHeap

Tries

Comes from retrieval

Other names: Digital, Radix, Prefix

O

  • Lookup O(L)
  • Insert O(L)
  • Delete O(L)

O(L) stands for Length of word, for word hello > 5

Implementations

  • Implement
  • Find longest common Prefix

[care, careful, car] -> car

Graphs

Node - vertex
Two directrly connected nodes - neighbours / adjacents
Can be directed or undirected Graphs

O

Implementations By

  • Adjacency matrix
Clara Sophie John
Clara 0 0 1
Sophie 1 0 0
John 1 1 0
  • Adjacency list

V stands for Vertixes

E stands for Edges
E = V * (V - 1) \(\approx\) \(V^{2}\) in the worst case scenario

K stands for Edges current node has
K = V in the worst case scenario

Matrix List List (worst case scenario)
Space O( \(V^{2}\) ) O(V+E) O( \(V^{2}\) )
Add Edge O(1) O(K) O(V)
Remove Edge O(1) O(K) O(V)
Query Edge O(1) O(K) O(V)
Find neighbours O(V) O(K) O(V)
Add node O(V) O(1) O(1)
Remove node O( \(V^{2}\) ) O( \(V^{2}\) ) O( \(V^{2}\) )
  • Check if has a cycle (all visiting visited)
  • Topological sorting
X > A B > P > r e s u l t [ X , A , B , P ] o r [ X , B , A , P ]

Undirected Graphs

  • Find the shortest distance (Dijkstra’s Shortest Path Algorithm)
  • Check if has a cycle
  • Minimum Spanning tree (Prim’s Algorithm)
3 A C - 1 - 2 - - 5 - - B D 4 A C - 1 - 2 - - 5 - - B D

Sorting

Bubble sort

Visualize

Best Worst
Passes O(1) O(n)
Comparisons O(n) O(n)
Total O(n) O( \(n^{2}\) )

Selection sort

Find the minimux value and swap it with first not sorted part of the array Visualize

Best Worst
Passes O(n) O(n)
Comparisons O(n) O(n)
Total O( \(n^{2}\) ) O( \(n^{2}\) )

Insertion sort

Visualize

Best Worst
Iterations O(n) O(n)
Shift items O(1) O(n)
Total O(n) O( \(n^{2}\) )

Merge sort

Visualize

Best Worst
Dividing O( \(\log{n} \) ) O( \(\log{n} \) )
Merging O(n) O(n)
Total O( \(n \log{n} \) ) O( \(n \log{n} \) )
Space O (n) O (n)

Quick sort

Maybe this sort algorithm is a default algorithm for most programming languages

Visualize

Best Worst
Partitioning O(n) O(n)
Number of Partitioning times O( \( \log{n} \) ) O(n)
Total O( \(n \log{n} \) ) O( \(n^{2} \) )
Space O ( \(n \log{n} \) ) O(n)

Counting sort

First non-comparison sort from above

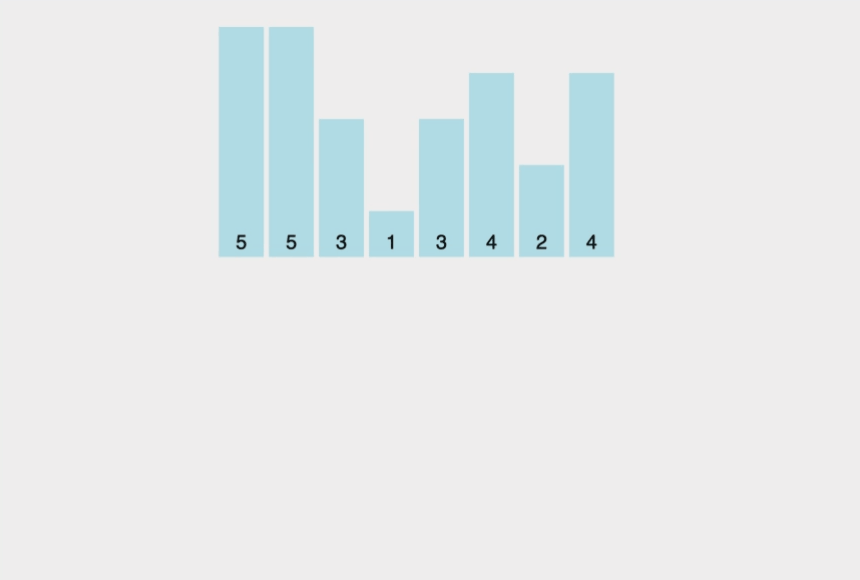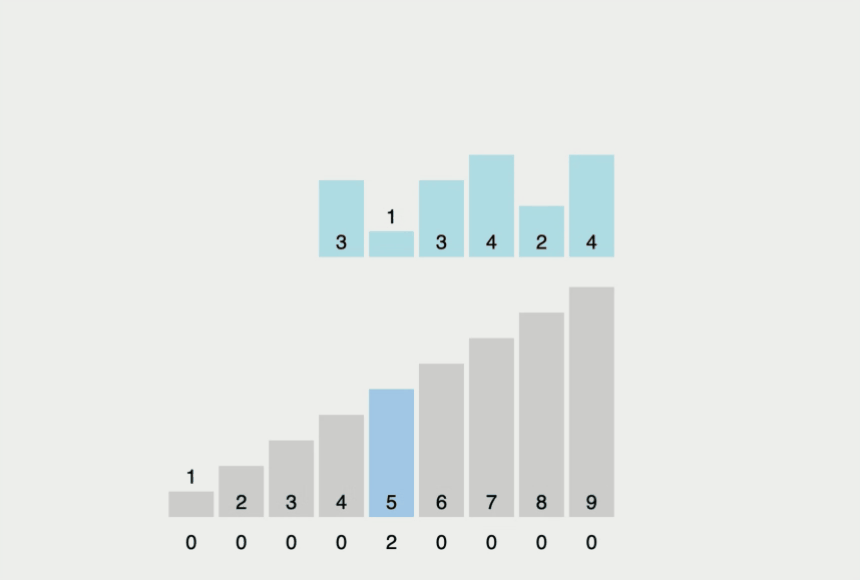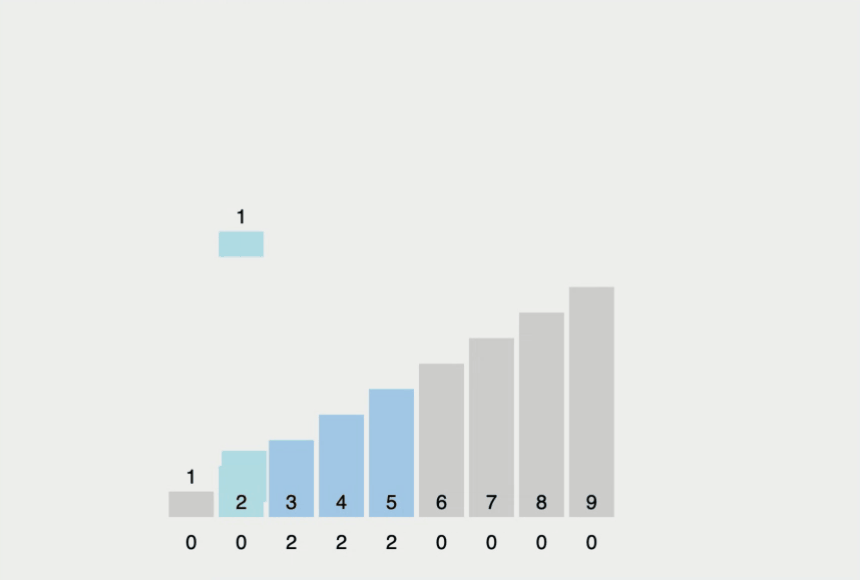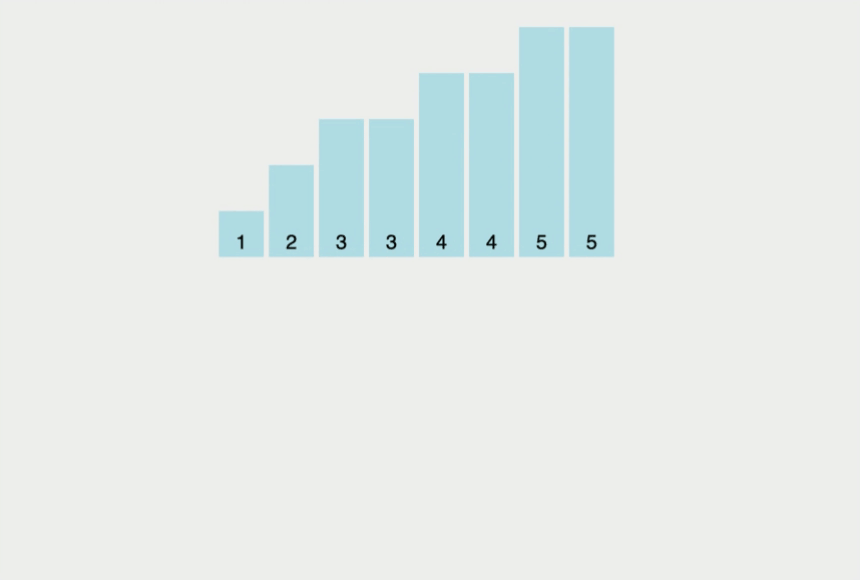
Visualize

Time O(n + K)
Space O(K)

Where K is the largest value in the array

Bucket sort

Best Worst
Distribution O(n) O(n)
Iteratin buckets O(K) O(K)
Sorting O(1) \( O(n^{2}) \)
Total O(n + K) \( O(n^{2}) \)
Space O(n + K)

Where K is the number of buckets

Searching

Best Worst
Time O(1) O(n)

Sorted collection

Best Worst
Time O(1) \( O(\log{n}) \)
Recursion Iteration
Space \( O(\log{n}) \) O(1)

It’s not faster than binary search Sorted collection

Best Worst
Time O(1) \( O(\log_3{n}) \)

Sorted collection

Best Worst
Time O(1) \( O(\sqrt{n}) \)

Sorted collection

Best Worst
Time O(1) \( O(\log{i}) \)

Where i is a position of target in the collection if it exists or not

String Manipulations

Popular tasks

1- Find the number of vowels in a string. Vowels in English are A, E, O, U and I.

Input: “hello”
Output: 2

2- Reverse a string.

Input: “hello”
Output: “olleh”

3- Reverse the order of words in a sentence.

Input: “Trees are beautiful”
Output: “beautiful are Trees”

4- Check if a string is a rotation of another string.

Input: “ABCD”, “DABC” (rotate one char to the right)
Output: true

Input: “ABCD”, “CDAB” (rotate two chars to the right)
Output: true

Input: “ABCD”, “ADBC”
Output: false

5- Remove duplicate characters in a string.

Input: “Hellooo!!”
Output: “Helo!”

6- Find the most repeated character in a string.

Input: “Hellooo!!”
Output: ‘o’

7- Capitalize the first letter of each word in a sentence. Also, remove any extra spaces between words.

Input: “trees are beautiful”
Output: “Trees Are Beautiful”

Input: “ trees are beautiful ”
Output: “Trees Are Beautiful”

8- Detect if two strings are anagram of each other. A string is an anagram of another string if it has the exact same characters in any order.

Input: “abcd”, “adbc”
Output: true

Input: “abcd”, “cadb”
Input: true

Input: “abcd”, “abcd”
Output: true

Input: “abcd”, “abce”
Output: false

9- Check if a string is palindrome. If we read a palindrome string from left or right, we get the exact same characters.

Input: “abba”
Output: true

Input: “abcba”
Output: true

Input: “abca”
Output: false